YouTube Kanal von Martin Wabnik
Dieser YouTube Kanal bietet über 400 hochwertige Mathematik-Videos zu verschiedenen Themen der Schulmatheamtik. Dabei geht es um ein tiefes Verständnis der Mathematik (deep learning) und nicht um die Bereitstellung sinnentleerter Lösungsrezepte. Hinter jedem Video steckt ein didaktisches Konzept, welches entschieden sprachlich und visuell umgesetzt wird. Jeder Mensch, der Mathematik wirklich verstehen möchte, wird hier das finden, wonach er lange gesucht hat.
https://www.youtube.com/@martinwabnik/playlists
Links zu einzelnen Videos
Hauptsatz der Differential – und Integralrechnung – anschauliche Erklärung
*(Genauer gesagt: Man kann die Fläche zwischen dem Graphen einer Funktion f und der x-Achse auf dem Intervall [a; b] durch die Differenz der Funktionswerte F(b) und F(a) einer Stammfunktion F bestimmen.)
Exponentialfunktion mit Salzteig
Ortsvektor – Definition
pq-Formel für quadratische Gleichungen
Kehrwertregel – anschauliche Erklärung
Kugeloberfläche – Kosmetik und Nanopartikel
Mathe einfach unterrichten – die relative Häufigkeit und ein folgenreicher Irrtum
In diesem Video wird gezeigt, wie sehr das Verständnis der Wahrscheinlichkeitsrechnung unter diesem Irrtum leidet, wie das vermieden werden kann und wie es wirklich ist. Und es wird gezeigt, wie einfach die dahinterliegende Mathematik tatsächlich ist.
Das empirische Gesetz der großen Zahlen gibt es in vielen Formulierungen, wobei manche falscher als andere sind. Völlig falsch ist die folgende Formulierung, die man auf den Seiten des Vereins MUED e. V. finden kann (wenn man Mitglied ist):
„Dieses berühmte Gesetz der Großen Zahl besagt, dass bei vielen unabhängigen Wiederholungen eines Zufallsexperiments, sei es Münzwurf, Würfeln, Lotto, Kartenspielen oder was auch immer, die relative Häufigkeit und die Wahrscheinlichkeit eines Ereignisses immer näher zusammenrücken müssen: Je häufiger wir eine faire Münze werfen, desto näher kommt der Anteil von ‚Kopf‘ seiner Wahrscheinlichkeit ein halb, je häufiger wir würfeln, desto näher kommt der Anteil der Sechsen der Wahrscheinlichkeit für Sechs, und je häufiger wir Lotto spielen, desto näher kommt die relative Häufigkeit der 13 der Wahrscheinlichkeit der 13. An diesem Gesetz gibt es nichts herumzudeuteln, dieses Gesetz ist in gewisser Weise die Krönung der gesamten Wahrscheinlichkeitstheorie.“
Um es ganz kurz zu machen: Wenn es dieses Gesetz in dieser Formulierung richtig wäre, gäbe es keinen einzigen (wiederholbaren) Zufallsversuch.
Kein Zufallsversuch
Ein Beispiel: Angenommen, wir werfen zufällig eine Münze, sodass wir die Ergebnisse Z (Zahl) und K (Kopf) erhalten können. Dabei sollen beide Ergebnisse jeweils die Wahrscheinlichkeit 0,5 haben. Nehmen wir weiter an, wir hätten die Münze 50-mal geworfen und hätten 50-mal Z erhalten. Dann war die relative Häufigkeit von Z nach der ersten Versuchsdurchführung gleich 1, nach der zweiten Versuchsdurchführung war sie ebenfalls gleich 1 und auch nach der dritten, vierten usw. In diesen ersten 50 Versuchsdurchführungen hat sich die relative Häufigkeit von Z also nicht der Wahrscheinlichkeit von Z angenähert.
Nun wird oft argumentiert, die Annäherung von relativer Häufigkeit und Wahrscheinlichkeit finde „auf lange Sicht“ oder auch bei „sehr vielen“ Versuchsdurchführungen statt. Aber was soll das bedeuten? Muss die Münze, wenn sie in den ersten 50 Versuchsdurchführungen zu oft Z angezeigt hat, bis zur 100-sten Versuchsdurchführung verstärkt K zeigen, damit sich das Verhältnis wieder ausgleicht? Oder muss sich die relative Häufigkeit erst bis zur 1000. Versuchsdurchführung der Wahrscheinlichkeit angenähert haben?
Wie wir es auch drehen und wenden: Wenn sich relative Häufigkeit und Wahrscheinlichkeit annähern müssen, darf das Ergebnis eines Münzwurfs irgendwann nicht mehr vom Zufall abhängen, sondern muss sich nach dem richten, was die Münze in den Versuchsdurchführungen davor angezeigt hat. Damit wäre der Münzwurf kein Zufallsversuch mehr. Man mag darüber streiten, was genau Zufall sein soll, aber mit Sicherheit gehört doch zu einem Zufallsversuch wie dem Münzwurf dazu, dass es eben kein Gesetz gibt, welches der Münze vorschreibt, was sie anzuzeigen hat.
Noch schlimmer wird die Lage, wenn im Anfangsunterricht der Stochastik behauptet wird, die Wahrscheinlichkeit eines Ereignisses sei die Zahl, zu der die relative Häufigkeit des Ereignisses strebt, wenn der Zufallsversuch oft genug wiederholt wird. Abgesehen davon, dass Schülern weder klar ist, was „streben“ oder „oft genug“ sein soll, können sie eine solche „Definition“ auch nicht mit ihrer Vorstellung von Zufall verbinden. Denn diese Herangehensweise führt zu der absurden Idee, dass irgendwer der Münze sagen muss, was sie zu machen hat oder dass die Münze ein Gedächtnis hat und selbst um den Ausgleich von relativer Häufigkeit und Wahrscheinlichkeit bedacht ist. Damit sind schon die grundlegenden Begriffe der Wahrscheinlichkeitsrechnung, nämlich Zufall und Wahrscheinlichkeit, derartig widersprüchlich, dass für Schüler ein Verständnis dieses Gebietes der Mathematik ausgeschlossen ist.
Überflüssige Statistik
Man kann in jedem Buch über die Einführung in die Wahrscheinlichkeitstheorie nachlesen, dass sich die relative Häufigkeit eines Ereignisses auch nach einer noch so großen Anzahl von Versuchsdurchführungen nicht an die Wahrscheinlichkeit des Ereignisses annähern muss. Alle statistischen Methoden, mit denen man von der relativen Häufigkeit auf die Wahrscheinlichkeit schließt, wären überflüssig, wenn sich die relative Häufigkeit der Wahrscheinlichkeit annähern müsste. Es gibt die „Konvergenz in Wahrscheinlichkeit“ und das schwache Gesetz der großen Zahlen nur deshalb, weil die relative Häufigkeit eines Ereignisses eben nicht analytisch gegen die Wahrscheinlichkeit des Ereignisses konvergiert. Warum aber trotzdem an deutschen Schulen falsche Mathematik unterrichtet wird, ist für mich persönlich nicht nachvollziehbar.
Was tatsächlich gilt
Es gilt das schwache Gesetz der großen Zahlen. Auf den obigen Fall angewendet bedeutet dieses Gesetz vereinfachend formuliert, dass sich die relative Häufigkeit nicht der Wahrscheinlichkeit annähern muss, sondern dass die Wahrscheinlichkeit der Annäherung steigt.
Etwas genauer: Wir können uns fragen, wie groß die Wahrscheinlichkeit ist, dass die relative Häufigkeit von Z in einem bestimmten Intervall um die Wahrscheinlichkeit von Z liegt. Da die Wahrscheinlichkeit von Z gleich 0,5 ist, können wir als Intervall z. B. (0,4; 0,6) festlegen. Die Wahrscheinlichkeit, dass die relative Häufigkeit von Z in diesem Intervall liegt, wird nun mit steigender Anzahl der Versuchsdurchführungen immer größer.
Stellen wir uns folgende Zufallsversuche vor: In einem Behälter befinden sich eine blaue und eine rote Kugel. Es wird eine Kugel zufällig gezogen, die Frabe notiert und die Kugel wieder zurück gelegt. Danach wird wieder eine Kugel zufällig gezogen usw.
Ist beim ersten Versuch eine rote Kugel gezogen worden, so ist die Wahrscheinlichkeit, beim zweiten Versuch eine rote Kugel zu ziehen, genauso groß wie beim ersten Versuch, nämlich 0,5. Das gilt auch für andere Versuchsanzahlen: Sind z. B. nach 99 Versuchen 99 rote Kugeln gezogen worden, ist die Wahrscheinlichkeit, beim 100. Versuch wieder eine rote Kugel zu ziehen, immer noch gleich 0,5. Und das gilt auch, wenn vorher 99 blaue Kugeln gezogen wurden oder wenn irgendeine andere Kombination blauer und roter Kugeln gezogen wurde.
Das bedeutet, die Wahrscheinlichkeit, 100 mal rot zu ziehen, ist genauso groß wie die Wahrscheinlichkeit, irgendeine andere Kombination aus blauen und roten Kugeln zu ziehen. Deshalb kann die relative Häufigkeit roter Kugeln nach 100 Versuchen bei 1 liegen. Damit ist sie maximal weit von der Wahrscheinlichkeit für rot entfernt und liegt nicht in der Nähe von 0,5. Die gleiche Argumentation gilt auch für 1 000, für 10 000 und für jede andere Anzahl von Versuchen. Es gibt also keine noch so große Anzahl von Versuchen, für die gilt: Die relative Häufigkeit der roten Kugeln muss in der Nähe von 0,5 liegen. Deshalb muss sich auch nicht die relative Häufigkeit der roten Kugeln bei zunehmender Anzahl der Versuchsdurchführungen der Wahrscheinlichkeit, eine rote Kugel zu ziehen, annähern.
Es wird behauptet, Jakob Bernoulli (1654 – 1705) habe das empirische Gesetz der großen Zahlen als erster formuliert. Das ist aber nicht richtig – zumindest dann, wenn man die gängigen Formulierungen berücksichtigt. Bernoulli schrieb z. B. nicht, die relativen Häufigkeiten eines Ereignisses A pendelten sich bei hinreichend großer Anzahl n der Versuchswiederholungen bei der Wahrscheinlichkeit von A ein. Ebensowenig schrieb er, die relativen Häufigkeiten eines Ereignisses A stabilisierten sich mit zunehmender Anzahl der Versuchsdurchführungen bei der Wahrscheinlichkeit von A und er schrieb auch nicht, die relativen Häufigkeiten von A müssten sich mit zunehmender Anzahl der Versuchsdurchführungen der Wahrscheinlichkeit von A annähern.
Und hier ist – in der deutschen Übersetzung – das, was Bernoulli tatsächlich schrieb:
„Satz: Es möge sich die Zahl der günstigen Fälle zu der Zahl der ungünstigen Fälle genau oder näherungsweise wie , also zu der Zahl aller Fälle wie \( \frac{r}{r+s}=\frac{r}{t} \) – wenn \( r+s=t \) gesetzt wird – verhalten, welches letztere Verhältniss zwischen den Grenzen \( \frac{r+l}{t} \) und \( \frac{r-l}{t} \) enthalten ist. Nun können, wie zu beweisen ist, soviele Beobachtungen gemacht werden, dass es beliebig oft (z. B. c-mal) wahrscheinlicher wird, dass das Verhältniss der günstigen zu allen angestellten Beobachtungen innerhalb dieser Grenzen liegt als ausserhalb derselben, also weder grösser als \( \frac{r+l}{t} \) , noch kleiner als \( \frac{r-l}{t} \) ist.“ (Bernoulli 1713, S. 104), in der Ausgabe: Wahrscheinlichkeitsrechnung (Ars conjectandi), Dritter und vierter Theil, übersetzt von R. Haussner, Leipzig, Verlag von Wilhom Engelmann, 1899)
Das, was Bernoulli schrieb, ist übrigens richtig und kommt dem schwachen Gesetz der großen Zahlen sehr nahe.
Es sind beliebig viele Situationen denkbar, in denen die relative Häufigkeit eines Ereignisses sich nicht der Wahrscheinlichkeit dieses Ereignisses nähert, sondern sich von diesem entfernt.
Ein Beispiel: Angenommen, wir werfen zufällig eine Münze, sodass wir die Ergebnisse Z (Zahl) und K (Kopf) erhalten können. Dabei sollen beide Ergebnisse jeweils die Wahrscheinlichkeit 0,5 haben. Nehmen wir weiter an, wir hätten die Münze 100-mal geworfen und 50-mal Z sowie 50-mal K erhalten. Dann ist die relative Häufigkeit von Z gleich 0,5. Wenn wir nun die Münze nochmals werfen, erhalten wir entweder Z – dann ist die relative Häufigkeit von Z gleich \(0,\overline{5049}\) – oder wir erhalten K – dann ist die relative Häufigkeit von Z gleich \(0,\overline{4851}\). In beiden Fällen entfernt sich die relative Häufigkeit Z wieder von der Wahrscheinlichkeit von Z. Wir können, nachdem wir beim Versuch Nummer 101 das Ergebnis Z erhalten haben, bei nachfolgenden Versuchsdurchführungen immer wieder Z erhalten. Die relativen Häufigkeiten für Z sind dann:
\(\approx 0,5098\), \(\approx 0,5146\), \(\approx 0,5192\), \(\approx 0,5283\), usw.
Damit rückt also die relative Häufigkeit von Z immer weiter von der Wahrscheinlichkeit von Z ab, was dem angeblichen Gesetz der großen Zahlen widerspricht.
Das empirische Gesetz der großen Zahlen wird oft damit begründet, dass zwar auch ungewöhnliche Ergebnisse vorkommen können, die seien aber so unwahrscheinlich, dass sie praktisch nie vorkommen. Z. B. sei beim 30-fachen Münzwurf das Ergebnis KKKKKKKKKKKKKKKKKKKKKKKKKKKKKK sehr ungewöhnlich und auch unwahrscheinlich, während das Ergebnis KZZKZKKKZKZZKZZZKKKZKZKKKZZZZK viel normaler und deshalb wahrscheinlicher sei.
Das ist nicht nur deshalb falsch, weil beide Ergebnisse genau die gleiche Wahrscheinlichkeit haben, sondern auch deshalb, weil wir Menschen das, was an bestimmten Ergebnissen ungewöhnlich sein soll, in die Ergebnisse hineinfantasieren. Anders gesagt: Die Münze „weiß“ nichts von ungewöhnlichen Ergebnissen. Schauen wir uns dazu ein Beispiel an:

Angenommen, wir haben 10 Kugeln mit den Ziffern von 0 bis 9. Die Kugel mit der 0 ist grün, alle anderen sind gelb. Wir ziehen zufällig zehnmal mit Zurücklegen und mit Reihenfolge.
Achteten wir nur auf die Farben, empfänden wir das Ergebnis

vermutlich nicht als ungewöhnlichn. Käme dann aber bei der Betrach-tung der Zahlen das hier zum Vorschein

gälte die Stichprobe aber wohl doch als ungewöhnlich.
Wenn wir wollen, können wir aber noch ganz andere Maßstäbe ansetzen: Eine Stichprobe soll als ungewöhnlich gelten, wenn die Ziffernfolge in den ersten Nachkommastellen von π vorkommt. Die Stichprobe

ist gewöhnlich, weil sie nicht einmal unter den ersten 200 Millionen Nachkommastellen von π vorkommt. Die Stichprobe

ist ungewöhnlich, weil sie an Position 3 794 572 vorkommt. Die Stichprobe

kommt sogar an Position 851 vor und ist damit quasi extrem ungewöhnlich.
Egal ob ungewöhnlich oder nicht: Die Wahrscheinlichkeit jeder Stichprobe ist exakt die gleiche, nämlich: \[\frac{1}{10\,000\,000\,000}\]
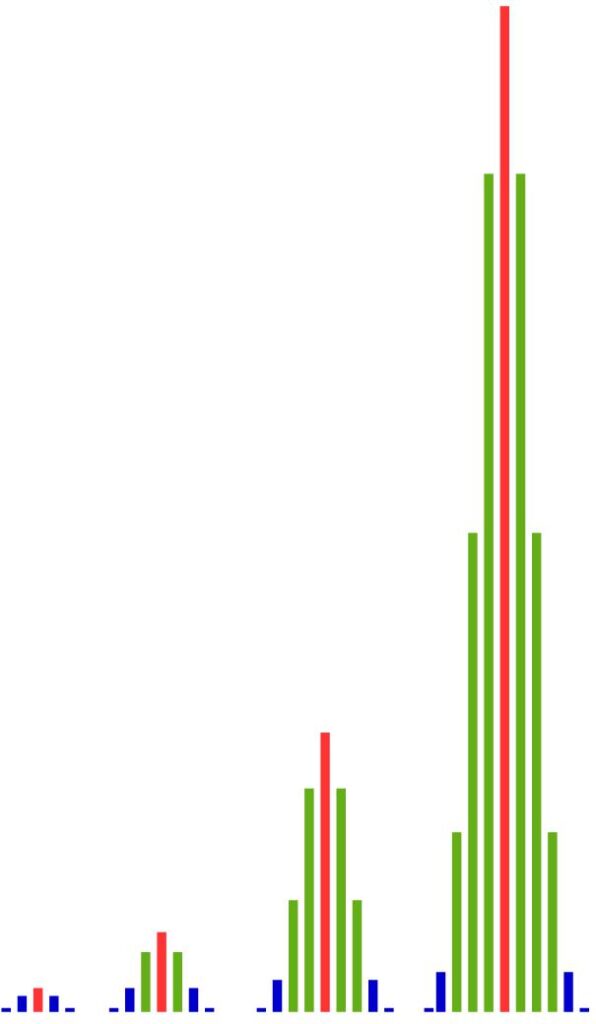
Schauen wir uns ein Beispiel dazu an: Wir ziehen zufällig eine Kugel aus einem Behälter, in dem sich zwei Kugeln befinden. Eine Kugel ist blau, die andere ist rot. Wir ziehen mehrmals mit Zurücklegen und mit Reihenfolge.

Wir wollen uns im Weiteren für die Anzahlen der roten Kugeln interessieren. In den folgenden Tabellen sind diese Anzahlen in Abhängigkeit von den Versuchsdurchführungen aufgelistet. Beim 8-maligen Ziehen gibt es z. B. 56 Ergebnisse mit 3 roten Kugeln.
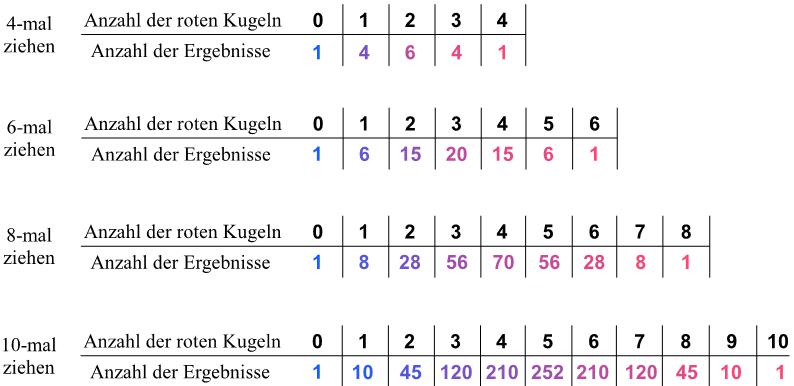
Diese Anzahlen werden von den Säulendiagrammen links maßstabsgetreu dargestellt. Wie wir sehen, wachsen mit zunehmender Anzahl der Versuchsdurchführungen die Anzahlen der Ergebnisse in der Mitte viel schneller als am Rand. Je öfter wir den Versuch durchführen, desto größer werden die Unterschiede zwischen der Mitte und dem Rand.
Das heißt: Es gibt einfach viel mehr Ergebnisse mit ungefähr 50 % roten Kugeln als es Ergebnisse mit viel weniger oder viel mehr roten Kugeln gibt. Und der Anteil der Ergebnisse in der Nähe der Mitte wird immer größer, je größer die Anzahl der Versuchsdurchführungen ist.
Dieses Phänomen können wir auch mit anderen Anteilen roter Kugeln in der Grundgesamtheit beobachten: Sind in der Grundgesamtheit zwei Drittel der Kugeln rot, sehen wir eine Häufung der Ergebnisse mit zwei Dritteln roter Kugeln.
Was wir hier sehen, können wir zwar etwas vereinfachend – aber nicht falsch – mit folgendem Satz zusammenfassen: Die relativen Häufigkeiten roter Kugeln sind in den meisten Ergebnissen so ähnlich wie die Wahrscheinlichkeit, eine rote Kugel zu ziehen.
Mit den Begriffen der Statistik hört sich das so an: Die meisten Stichproben sind so ähnlich wie die Grundgesamtheit.
Wenn wir also eine Münze 100-mal werfen und wir ca. 50-mal K erhalten, liegt das nicht daran, dass sich die relative Häufigkeit stabilisiert oder die Münze auf einen Ausgleich zwischen K und Z bedacht ist oder daran, dass eine dunkle Macht den Fall der Münze beeinflusst, sondern schlicht und ergreifen daran, dass es viel, viel mehr Ergebnisse gibt, die ca. 50-mal K enthalten als es Ergebnisse gibt, die viel weniger oder viel mehr K enthalten.
Was ist Wahrscheinlichkeit?
Hilfe! Mein Kind kann kein Mathe!
Leider sehe ich immer wieder, dass aus z.B. einer 5 in Mathe in viel größeres Problem gemacht wird, indem das Kind im Extremfall sogar für krank erklärt wird und anschließend von einer Dyskalkulietherapeutin behandelt werden muss.
Wertschätzender Umgang und eine optimistische Einstellung können die Sache aber auch das sein lassen, was sie ist: Eine Zahl unter einer Klassenarbeit.